HISTORY
Classic Textbook
problem:
A vertical chain hangs just above a balance. It is dropped. What is the force read by the balance? [1,2]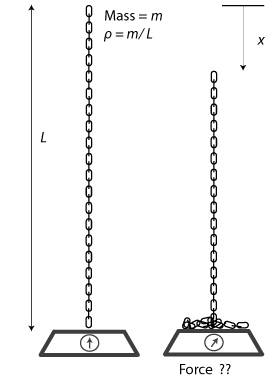
A vertical chain hangs just above a balance. It is dropped. What is the force read by the balance? [1,2]

Common answer:
At any time, the force registered is 3 times weight of chain on the balance = 3ρxg ;
How:
Here is the way this problem has been solved in most of the textbooks, under the category of 'variable mass' problems.
Consider an increment
of chain dx going from speed v to a stop in time dt.
Then:
Force on table
= weight of chain on table + impulsive force of increment dx colliding with the table
= ρxg + (mass) (change in speed) / (time taken)
= ρxg + (ρdx) (v) / (dt)
= ρxg + ρv2
= ρxg + ρ (2gx) (Assume: chain's part in air has fallen freely with g over a distance x, so v2 = 2gx )
= 3ρxg
But
there is
something missing in this analysis.
References:
[1] A.E.H. Love, An Introductory Treatise on Principles of Dynamics (Cambridge Univ. Press, Cambridge, 1897). Page 301-304.
[2] H. Lamb, Dynamics, 2nd Ed (Cambridge Univ. Press, London 1929). Page 149.
[1] A.E.H. Love, An Introductory Treatise on Principles of Dynamics (Cambridge Univ. Press, Cambridge, 1897). Page 301-304.
[2] H. Lamb, Dynamics, 2nd Ed (Cambridge Univ. Press, London 1929). Page 149.
This page was
updated on March 13, 2011